|
|
When Rules Seem Less Than Golden
|
|
|  |
by Michael Buchler
Florida State University
Tallahassee, Florida
|
|
| | Fostering a Deeper Understanding of Musical Composition
As teachers, we have surely all had diligent students who, as the
saying goes, fail to see the forest for the trees. In the music theory
classroom, we frequently see students who struggle so vehemently to
abide by every part-writing maxim and to avoid every pitfall that they
lose sight of the ultimate goal: creating something that sounds musical
and stylistic and thereby coming to a deeper understanding of musical
composition.
The rigidity of our rules often lies at the
heart of this problem. Rather than teaching tonal part-writing as the
amalgamation of large sets of fixed rules, it can be more beneficial to
focus upon a relatively small collection of general principles. This is
less taxing on the students' memory, and it tends to foster a more
musical environment. For one thing, rules are often presented as bad
things to avoid rather than good features to strive toward: don't write
parallel fifths, don't double the leading tone, don't write big leaps,
don't forget your accidentals. Such admonitions can obscure the
enjoyable aspects of music, and they seem less productive than
emphasizing broader aspects of style like how to write a good melody or
a strong cadence.
One of the most common sets of rules taught
in theory classrooms and emphasized in many popular textbooks deals
with chord doubling. Without question, the majority of the time
students would be well advised to double the root of a root position
chord. Steven Laitz's recent textbook, The Complete Musician: An Integrated Approach to Tonal Theory, Analysis, and Listening,
sensibly directs students to "double stable tones. If possible, double
the root.... If it is not possible to double the root, double the
fifth. Doubling the third (except in V) is the final option."
As general guidelines, Laitz's suggestions seem reasonably sound, but
other textbooks depict far more prescriptive conventions. They often
ask students to memorize lists of what tone should be doubled in every
particular triad, regardless of musical context. Such hard and fast
rules are, in a certain sense, comforting for both students and
teachers. They impart a feeling that there is a formula for doing it
right -- if only I can learn (or get my students to learn) its many
facets.
Of course, we all know that such part-writing
strictures invariably demand a set of exceptions. Each exception might
seem like a relatively small piece of information that is easily
grasped, but the stack of rules and exceptions can really add up over a
semester or two. Here's a piece of the daunting part-writing formula
that surely floats around in some students' brains:
Always double the root of a chord. Never double the leading tone, so
don't double the root if the root is the leading tone. Don't double the
third, except if the chord is diminished, in which case it's good to
double the third. Doubling the third might be okay if I am writing a
secondary triad (ii, iii, vi, and viiº), but probably not if the chord
is minor. Don't double the fifth of a chord, except if it is a second
inversion triad, then you should double the fifth. Never double the
seventh. What seems especially frightening is that those
"rules" are all relatively general (i.e., they mostly do not deal with
individual chords) and that these rather specific generalities only
deal with doubling rules. There are far more such rules that govern
harmonic progression. They can be a topic for another time, however.
A student can easily get buried in rules, and obedient students who
doggedly memorize and adhere to "the rules" frequently produce
grammatically "correct" yet utterly unmusical creations. Where the
rules do not work, we tend to provide exceptions. Double the third of a
VI chord at a deceptive cadence. Double the third of the ii chord when
in minor (or perhaps when it's in first inversion). The seventh can go
up in the progression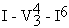 
. The leading tone can go down a third if it's in the inner voice. The leading tone can go down when moving from V6
to vi in major. Of course, we also don't want to introduce too many
exceptions, having seen the products of students who take too many
liberties before they understand the basics of tonal composition.
I believe that rules governing chord doubling are particularly
overtaught and can actually damage a student's understanding of tonal
structure. Doubling rules frequently are not context specific, and they
emphasize vertical structures over linear patterns.
To see
the sorts of problems that can arise when students have to weigh
different sorts of rules, we will look at how the following chord
progression might be harmonized. It could easily come from an AP Exam
(note that I use the convention of showing the cadential six-four as a
dominant chord; some readers will be most familiar with it as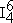 
):
Example 1 (below) shows a realization of this harmonic progression by a
good (if fictional) student, who is trying to double the root of each
triad. The only exception she makes is at the deceptive cadence. As a
good student, she knows all too well that one must double the third of
the submediant in a deceptive motion to avoid those insidious forbidden
parallels. (That is a doubling convention that I wholeheartedly endorse
teaching, and one that a lot of students resist learning. How many
times have you seen the leading tone unresolved at the deceptive
cadence and/or parallel fifths and/or parallel octaves at that
location? And if students blow the cadence, they are penalized heavily
on the AP Exam, especially in the counterpoint/melodic harmonization
exercise).
Example 1: The progression with root doublings
Our student could well look at the above exercise and see that it might
be easier had she started with C in the soprano voice. Such a
realization is provided in Example 2. Even here, we have an
unattractive leap from Bb to F in the soprano. That one break in
melodic smoothness is pretty unmusical, even though no rule has been
broken. Likewise, the tenor seems unnecessarily leapy and bizarre. It
might get a good grade, but does anyone really want to hear it?
Example 2: The progression with root doublings, starting on C in the soprano
Example 3 features a realization by an (again fictional) student who
has been taught to prioritize smooth voice leading, independence of
line, and singability. In other words, a minimum number of rules. We
can see here that the root is still the most commonly doubled chord
member. That's just the way the deck is stacked in tonal composition.
We don't really need rules to tell us this, although we certainly do
need rules to tell us not to double active tones.
Example 3: The progression with a nicer melody, starting on C in the soprano
Example 4 presents another perfectly fine realization of this
progression. This time our student (who has not devoted her time to the
memorization of doubling strictures) begins with the third on top. This
attempt doubles the chordal fifth a couple of times, which many
teachers forbid, but the result is something that would put a smile on
any AP Exam Reader's face.
Example 4: The progression with a nice melody, starting on A in the soprano
Perhaps the best melody for this progression utilizes one of the most common melodic formulas associated with the progression
the melodic pattern of scale degrees 3-4-5 (mi-fa-sol).
If a student saw and recognized that musical pattern, she might well
have decided to begin the melody on tonic, moving up the scale by step.
If that student was concerned with doubling conventions, however, she
might well produce the realization found in Example 5, which starts
well, but ends badly with an unmusical melodic leap (written to avoid
doubling the third of a chord) and tough-to-avoid parallel fifths in
the inner voice.
Example 5: Nice melody to start, but then trouble ensues
To avoid that ugly soprano leap in measure 2, a student would be better
off writing a stepwise descent from C. This necessitates doubling the
third of the ii6 chord (frequently a good idea in any case),
and a preference for smooth inner voices might also lead to doubling
the third in the I6 chord. See Example 6 for this rendition, which to me seems the best of the bunch.
Example 6: Nice melody to start, and then good melodic closure
I would not want to leave the impression that I avoid teaching rules.
Nothing could be further from the truth. But when guidelines and
generalities (such as most doubling conventions) are presented as
gospel, there can be deleterious effects: students begin prioritizing
vertical writing over counterpoint, they lose the ability to get
themselves out of part-writing jams, and perhaps worst of all,
part-writing becomes a rigid and academic task that requires little, if
any, musical judgment. Instead of dwelling on rules, I continually
emphasize the following three fundamental principles:
- All parts should be easily singable, and each part should have its own identity.
- Tendency tones (or active tones) should be resolved and should not be doubled.
- The
soprano part should have a nice melody, mostly moving by step; the
inner parts should avoid leaping and should preserve common tones when
possible.
With these principles firmly in place, students
require far less guidance and are able to move through material more
quickly and with greater confidence. Also, they do not tend to see the
enterprise of part-writing as arbitrary. In other words, they are far
more likely to see and appreciate both the forest and the trees.
Michael
Buchler is assistant professor of music theory at Florida State
University. Previously, he taught at the University of Iowa and Indiana
University, Bloomington. He was awarded campuswide teaching awards at
both Iowa and Florida State. His holds a Ph.D. in music theory from the
University of Rochester, Eastman School of Music, and M.M. and B.M.
degrees from the University of Michigan and the University of
Cincinnati. He has served as a Reader for AP Music Theory since 1998.
|
|
|
Starting an AP Program